Gidhub BE Developer

함수적 종속성 (Functional Dependency)

2017-10-10
goodGid
DB

Concept

  • 어떤 테이블 R에서 X와 Y를 각각 R의 속성 집합의 부분 집합이라 하자.

  • 속성 X의 값 각각에 대해

    시간에 관계없이 항상 속성 Y의 값이 오직 하나만 연관되어 있을 때

    Y는 X에 함수적 종속 또는 X가 Y를 함수적으로 결정한다고 하고

    X -> Y로 표기한다.

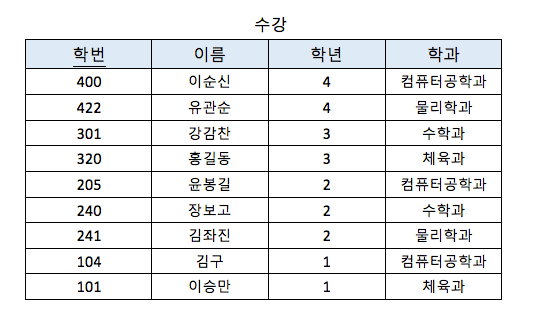
  • 수강 테이블에서 이름, 학년, 학과는 각각 학번 속성에 함수적 종속이다.
학번 --> 이름
학번 --> 학년
학번 --> 학과 
=> 학번 --> 이름, 학년, 학과

  • X -> Y의 관계를 갖는 속성 X와 Y에서

    X를 결정자(Determinant) / Y를 종속자(Dependent)라고 한다.

함수적 종속 다이어그램

학번, 과목번호 --> 성적
학번 --> 학년

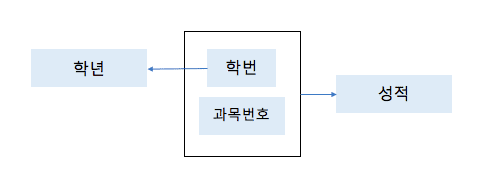
  • 수강 테이블의 속성 중 성적은 (학번, 과목번호)에 완전 함수적 종속이라 한다.

  • 수강 테이블의 속성 중 학년은 (학번, 과목번호)에 완전 함수적 종속이 아니므로 부분 함수적 종속이라 한다.

완전 & 부분 함수적 종속의 이해

  • 완전 함수적 종속이라는 말은 어떤 속성이 기본키에 대해 완전히 종속적 일 때를 말한다.

  • 부분 함수적 종속이라는 말은 기본키가 2개 이상 구성된 합성키이고

    합성키를 구성하는 하나의 속성에 함수적 종속성을 갖을 때 부분 함수적 종속이라 한다.

예를 들어 수강 테이블은 (학번, 과목번호)가 기본키 인데
성적은 학번과 과목번호가 같을 경우에는 항상 같은 성적이므로
즉 성적은 학번과 과목번호에 의해서만 결정되기 때문에 성적은 기본키(학번, 과목번호)에 완전 함수적 종속이다.

반면 학년은 과목번호에 관계없이 학번이 같으면 항상 같은 학년이므로
즉 기본키의 일부인 학번에 의해서 학년이 결정되기 때문에 학년은 부분 함수적 종속이다.

Recommend

Index