자료 구조(Data Structure) 구현

To Do
Stack
Queue
Tree
Sort
바이너리 서치(Binary Search)
출처

To Do

STL을 사용하지 않고 자료 구조를 구현해보자.

Stack

#include <iostream>
using namespace std;

int stack[10001];
int top = -1;

void push(int x){
    stack[++top] = x;
}

int empty() {
    if( top < 0 )
        return 1;
    else
        return 0;
}

void pop() {
    if (empty() == 1)
        cout << "-1" << "\n";
    else {
        cout << stack[top] << "\n";
        stack[top--] = 0;
    }
}

void size(){
    cout << top + 1 << "\n";
}

int main() {
    int n;
    cin >> n;
    for (int i = 0; i < n; i++) {
        string s;
        cin >> s;
        
        if( s == "push"){
            int x;
            cin >> x;
            push(x);
        }
        else if ( s == "top") {
            if (empty() == 1)
                cout << "-1" << "\n";
            else
                cout << stack[top] << "\n";
        }
        else if ( s == "pop") {
            pop();
        }
        else if ( s == "empty") {
            cout << empty() << "\n";
        }
        else if ( s == "size") {
            size();
        }
    }
    return 0;
}

출처

Queue

const int size = 10;
int queue[size];

int q_front;
int q_rear;

void QueueInit(){
    q_front = q_rear = 0;
}

int QueueSize(){
    return q_rear - q_front;
}

void QueuePush(int value){
    queue[q_rear++ % size] = value;
}

int QueuePop(){
    if(q_front == 0)
        return -1;
    return queue[q_front++];
}

bool QueueEmpty(){
    if( q_front == q_rear )
        return true;
    return false;
}

Tree

typedefstruct node{
   int data;
   struct node* leftchild;
   struct node* rightchild;
};

node* Make_Tree(int key) {
   node* Newnode = (node*)malloc(sizeof(node));
   Newnode->data = key;
   Newnode->leftchild =NULL;
   Newnode->rightchild =NULL;
   
   Newnode->leftchild = Make_Tree();
   Newnode->rightchild = Make_Tree();
   return Newnode;
}

Sort

선택 정렬

#include<iostream>
using namespace std;

void swap(int *arr, int a, int b){
    int tmp = arr[b];
    arr[b] = arr[a];
    arr[a] = tmp;
}

void SelectionSort(int *arr, int begin, int end){
    for(int i=begin; i<end; i++){
        int tmp = i;
        for(int j=i+1; j <= end; j++)
            if( arr[tmp] > arr[j] )
                tmp = j;
        if( tmp != i )
            swap(arr,i,tmp);
    }
}


int main(){
    int arr[5] = {5,2,1,4,3};
    SelectionSort(arr, 0, 4);
    return 0;
}

버블 정렬

#include<iostream>
using namespace std;

void swap(int *arr, int a, int b){
    int tmp = arr[b];
    arr[b] = arr[a];
    arr[a] = tmp;
}

void BubbleSort(int *arr, int begin, int end){
    for(int i=end; i>begin; i--){
        for(int j=begin; j<i; j++)
            if(arr[j] > arr[j+1])
                swap(arr, j, j+1);
    }
}

int main(){
    int arr[5] = {5,2,1,4,3};
    BubbleSort(arr, 0, 4);
    
    for(int i=0; i<5; i++)
        cout << arr[i] << endl;
    return 0;
}

삽입 정렬

#include <iostream>
using namespace std;

void swap(int *arr, int a, int b){
    int tmp = arr[b];
    arr[b] = arr[a];
    arr[a] = tmp;
}
void InsertSort2(int *arr, int begin, int end){
    for(int i=begin+1; i<=end; i++){
        int j;
        int v = arr[i];
        
        for(j=i; j>begin && arr[j-1] > v; j--)
            arr[j] = arr[j-1];
        
        if( i != j)
            arr[j] = v;
    }
}

void InsertSort(int *arr, int begin, int end){
    for(int i=0; i<end; i++){
        for(int j=i+1; j>=0; j--){
            if( arr[j-1] > arr[j])
                swap(arr, j-1, j);
        }
    }
}

int main(){
    int arr[5] = {5,2,1,4,3};
    InsertSort(arr, 0, 4);
    return 0;
}

퀵 정렬

#include<iostream>
using namespace std;

void swap(int *arr, int a, int b){
    int tmp = arr[b];
    arr[b] = arr[a];
    arr[a] = tmp;
}

void QuickSort(int *arr, int begin, int end){
    int pivot = begin;
    int left = begin;
    int right = end;
    
    while (left < right) {
        while (arr[left] <= arr[pivot] && left < end)
            left += 1;
        while (arr[right] >= arr[pivot] && right > begin)
            right -= 1;
        if( left < right ){
            swap(arr, left, right);
            continue;
        }
        swap(arr, pivot, right);
        QuickSort(arr, begin, right-1);
        QuickSort(arr, right+1, end);
    }
}

int main(){
    int arr[5] = {5,2,1,4,3};
    QuickSort(arr, 0, 4);
    return 0;
}

합병 정렬

#include<iostream>
using namespace std;

void MergeArray(int *arr, int *copy, int start, int end){
    int mid = (start + end ) >> 1;
    int i = start;
    int j = mid+1;
    int k = start;
    while (i <= mid && j <= end) {
        if( arr[i] <= arr[j])
            copy[k++] = arr[i++];
        else
            copy[k++] = arr[j++];
    }
    while (i <= mid)
        copy[k++] = arr[i++];
    while (j <= end)
        copy[k++] = arr[j++];
    
    for(int i=start; i<=end; i++)
        arr[i] = copy[i];
}
    
void MergeSort(int *arr, int *copy, int start, int end){
    if(start == end)
        return ;
    int mid = (start + end) >> 1;
    MergeSort(arr, copy, start, mid);
    MergeSort(arr, copy, mid+1, end);
    MergeArray(arr, copy, start, end);
}
int main(){
    int arr[5] = {5,1,4,3,2};
    int arr2[5];
    
    MergeSort(arr, arr2, 0, 4);
    for(int i=0; i<5; i++)
        cout << arr2[i] << endl;
}

합병 정렬은 O(NlogN)이기 때문에 성능이 준수하다.
다만 30개 이하의 숫자를 정렬할 때는 삽입 정렬과 별 차이가 없고 정렬하는데 추가적인 메모리가 필요하다는 단점이 있다.

보통은 재귀 함수를 사용해서 만든다.
합병 정렬은 분할 정복 알고리즘에 속한다.
유명한 수학자 폰 노이만이 개발했다.
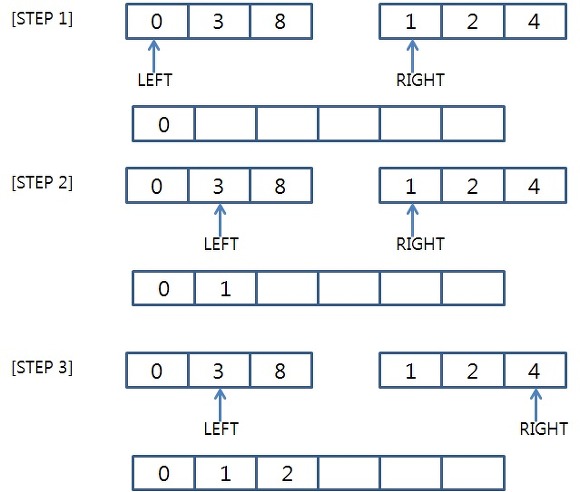
합병 정렬은 배열을 두 개로 나누고, 나눈 것을 다시 두 개로 계속 나눠 정렬한다.
합병 정렬의 단점은 array 외에도 result라는 추가적인 저장 공간이 필요하다는 것이다.
그래서 메인 메모리의 반이상의 배열 크기를 갖는다면 메인 메모리 내에서 사용할 수 없다.
외부 정렬 방식의 하나이다.
외부 정렬이란?
데이터의 크기가 주기억장소보다 클 경우 외부 기억장치(디스크, 테이프 등)을 사용하여 정렬하는 방식이다.
참고로 일부 브라우저에서는 배열.sort()를 할 때 합병 정렬을 사용한다고한다.

힙 정렬

#include<iostream>
using namespace std;

void swap(int *arr, int a, int b){
    int tmp = arr[b];
    arr[b] = arr[a];
    arr[a] = tmp;
}

void Heapify(int*arr, int index, int size) {
    for (int ch = (index << 1) | 1; ch <size; index = ch, ch = ch << 1 | 1) {
        if (ch + 1<size&& arr[ch + 1] > arr[ch])
            ++ch;
        if (arr[ch] <= arr[index])
            return;
        
        swap(arr,ch, index);
    }
}

void HeapSort(int*arr, int begin, int end) {
    int *base = arr + begin;
    int size = end - begin + 1;
    
    for (int i = size / 2 - 1; i >= 0; i--)
        Heapify(base, i, size);
    
    while (--size >= 1) {
        swap(arr,0, size);
        Heapify(base, 0, size);
    }
}

int main(){
    int arr[5] = {5,2,1,4,3};
    HeapSort(arr, 0, 4);
    return 0;
}

바이너리 서치(Binary Search)

#include<iostream>
using namespace std;

/*
 BS function return target index
 */
 int BS(int *arr, int _end, int target){
    int st = 0;
    int end = _end;
    int mid;
    
    while (st <= end) {
        mid = ( st + end ) >> 1;
        if( target == arr[mid] )
            return mid;
        else if( target > arr[mid] )
            st = mid + 1;
        else
            end = mid - 1;
    }
    return -1;
}

int main(){
    // arr은 정렬된 상태여야 한다.
    int arr[5] = {1,2,3,4,5};
    printf("%d\n", BS(arr, 4, 2)); // 1
    printf("%d\n", BS(arr, 4, 6)); // -1
    printf("%d\n", BS(arr, 4, 4)); // 3
}

출처

합병(머지, 병합) 정렬

자료 구조(Data Structure) 구현

To Do

Stack

Queue

Tree

Sort

선택 정렬

버블 정렬

삽입 정렬

퀵 정렬

합병 정렬

힙 정렬

바이너리 서치(Binary Search)

출처

Recommend