Gidhub BE Developer

다익스트라(Dijkstra) 알고리즘

2018-09-21
goodGid
Algorithm

다익스트라 알고리즘이란?

  • 다익스트라 알고리즘(Dijkstra’s algorithm)은 최단 경로(Shortest Path)를 찾는 대표적인 기법 가운데 하나이다.

  • 하나의 시작 정점으로부터 모든 다른 정점까지의 최단 경로를 찾는 알고리즘이다.

  • 다익스트라 알고리즘은 너비우선탐색(BFS)을 기본으로 한다.

  • 음수 가중치가 포함되어 있다면 사용할 수 없다.

  • 경로 탐색을 위한 알고리즘(DFS,BFS)는 가중치가 있을 때 최단 거리를 표현하기가 어렵다.

  • 그렇기 때문에 다익스트라 알고리즘이 생겼다.

동작 과정

  • Dijkstra의 알고리즘에서는 시작 정점에서 다른 정점으로 가는 최단 거리를 기록하는 배열이 반드시 있어야 한다.

  • 단, 정점 v에서 정점 w로의 직접 간선이 없을 경우에는 무한대의 값을 저장한다.

  • 알고리즘이 진행되면서 최단 거리가 발견되는 정점들이 집합 S에 하나씩 추가될 것이다.

  • 알고리즘의 매 단계에서 집합 S 안에 있지 않은 정점 중에서 가장 Distance 값이 작은 정점을 S에 추가한다.

  • 말 보단 그림으로 이해를 해보자.

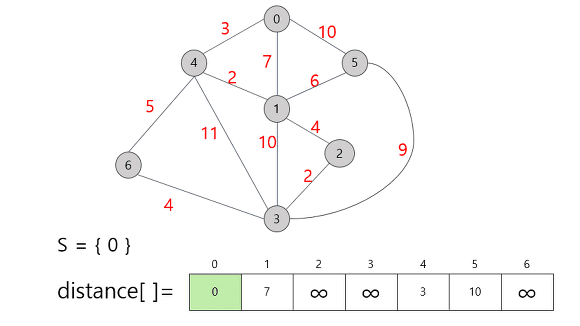
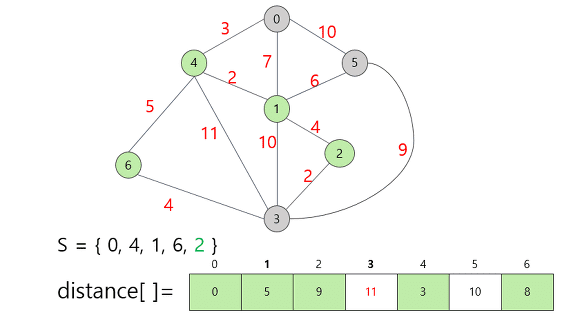
  • 시작 정점을 0으로 잡고, 각 지점까지의 거리를 표시했다.

  • 직접적으로 가는 경로가 없는 경우 무한대로 표시되어 있다.

  • 표시 되어 있는 거리 중 가장 짧은 거리는 정점 4까지의 거리인 3이므로 정점 4를 집합 S에 추가시켜준다.

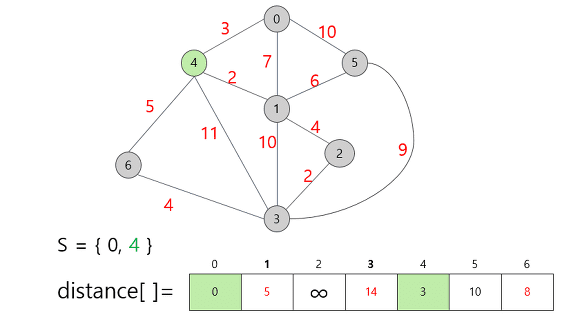
  • 새로운 정점이 S에 추가되면 다른 정점들의 Distance값이 변경된다.

  • 0번 정점에서는 직접적으로 갈 수 없던 정점에 새롭게 들어온 정점 4를 통해 직접적으로 갈 수 있기 때문에 무한대의 값에서 구체적인 정수거리로 정보가 갱신됐다.

  • 또한 새로운 정점 4를 통해 갈 때 더 짧은 경로가 발견 된다면 그 정보 또한 갱신을 해준다.

  • 구체적으로는 위의 0번 정점만을 선택했을 때, 1번 정점까지의 거리가 7이였는데, 4번 정점을 택함으로써 이 거리가 5로 줄어들었다.

  • 즉 더 짧은 거리가 나타나거나 기존의 무한대에서 직접 경로가 생겼을 때 거리(비용)값을 갱신해준다.

  • 갱신된 정보들을 바탕으로 집합 S에 추가할 다음 정점을 선택해보자.

  • 남은 정점 중 가중치가 가장 적게 표시되어 있는 건 정점 1이다. (Distance 배열에 있는 값들 중 최소 값)

  • 1번 정점을 집합 S에 추가하고, 갱신할 수 있는 정보가 있다면 갱신해주자.

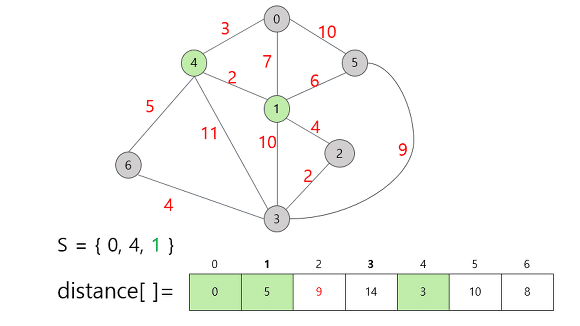
  • 갱신된 정보는 2번 정점에 대한 가중치다.

  • 1번 정점을 추가함으로써 2번 정점까지 직접적으로 갈 수 있게 되었으므로 무한대의 값에서 구체적인 가중치인 9로 수정해준다.

  • 다음으로, 현재까지의 Distance 배열값을 기준으로 가장 작은 값은 6번 정점의 8이므로, 6번 정점을 택한다.

  • 마찬가지로 갱신할 수 있는 정보는 갱신해준다.

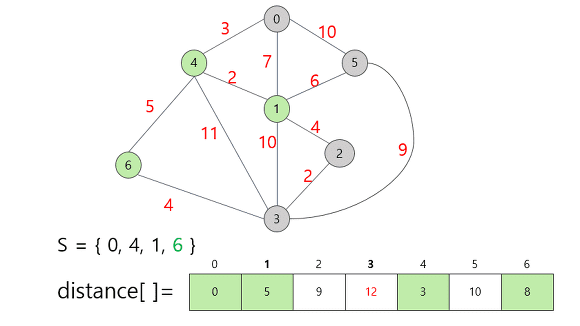
  • 6번 정점을 집합 S에 추가함으로써 갱신할 수 있는 정보는 정점 3까지의 거리다.

  • 기존의 14에서 12로 거리가 단축되었으므로 이 값을 갱신했다.

  • 이제 다음에 택할 정점을 생각해보자.

  • Distance 배열에서 가장 작은 가중치는 9이므로 정점 2를 택한다.

  • 정점 2를 집합 S에 추가함으로써 정점 3까지의 거리가 갱신되었다.

  • 남은 두 개의 과정은 그림을 올리지 않아도 유추가 가능하다.

  • 가중치가 가장 적은 5번 정점을 선택하고, 갱신할 정보가 있다면 갱신한다.

  • 그 다음은 마지막 정점인 3번 정점을 택한다.

  • 다익스트라 알고리즘은 위와 같은 순서와 원리로 진행된다.

다익스트라 단점

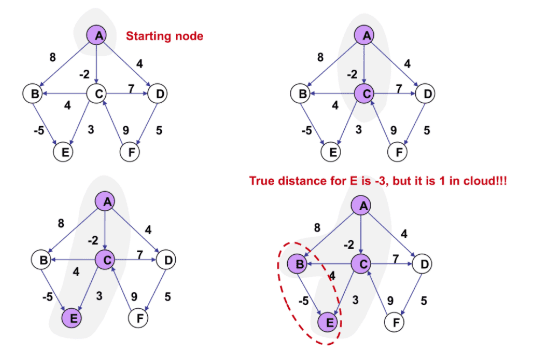
왜 음의 가중치는 계산을 못할까?

  • 결론적으로 말해서 그 이유는 이전 노드까지 계산해둔 최소거리 값이 최소라고 보장할 수 없기 때문이다.

  • 다익스트라는 정점을 지날수록 가중치가 증가한다라는 사실을 전제하고 쓰여진 알고리즘이다.

  • 하지만 음의 가중치가 있다면 정점을 지날수록 가중치가 감소할 수도 있다는 의미가 되므로 앞선 전제가 무너진다.

  • 그러므로 다익스트라 알고리즘에서는 음의 가중치를 계산할 수 없다.

  • 하지만 이와같은 점을 음의 가중치에서도 최소거리를 계산하는 벨만-포드 알고리즘이 존재한다.

Why?

왜 우선순위 큐를 쓸까?

  • 결론적으로 말해서 최소거리 값 갱신 횟수의 증가 때문이다.

  • 먼저 우선순위 큐를 쓰지 않고 일반 큐를 써도 결과에는 차이가 없다.

  • 하지만 우선순위 큐를 쓰는 이유는 속도에 이점이 있기 때문이다.

  • 다익스트라 알고리즘에서 속도에 영향을 주는 요소는 큐에서 노드를 꺼내오는 횟수와 우선순위 큐의 갱신 횟수이다.

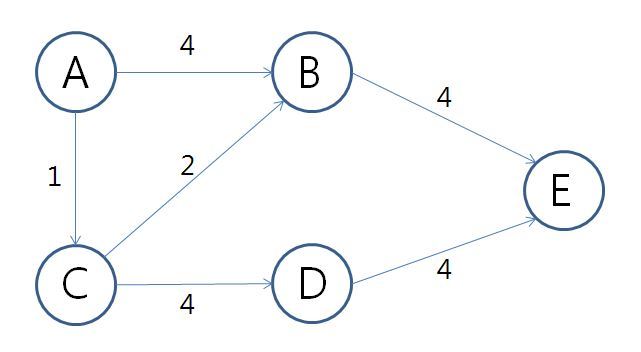
예를 들면 
만약 위의 예제에서 일반 큐를 쓴다면 
A에서 검사를 시작할 때, 연결된 두 노드 B와 C중 B부터 검사한다. 

하지만 우선순위 큐라면 C부터 검사한다. 
왜냐하면 우선순위 큐로 인해 최소 거리로 정렬된 순서로 큐에서 추출되기 때문이다. 

이 상황을 정리하면 A에서 E까지 최소거리를 검사할 때

일반 큐)
A -> B -> C -> E -> B -> D -> E -> E 순으로 검사
첫 번째 E 노드를 검사할 때, 현재 B까지 최소거리는 4, C까지 최소거리는 1, E까지 최소거리는 8이 된다.
하지만 그 다음 B노드를 검사할 때 B의 최소거리가 3으로 갱신되기 때문에 이전에 계산한 작업이 무의미한 값이 된다. 
이런 경우가 일반 큐를 사용할 때 나타나는 시간상의 비효율적인 대표 예이다.

우선순위 큐)
A -> C -> B -> B -> D -> E -> E -> E 순으로 검사
이 검사는 이전에 계산해둔 값이 그 단계에서 최소값이라는 것이 보장되기 때문에 갱신 횟수가 현저히 적어진다.

이해를 돕기위한 작은 예지만 그래프의 크기가 커지면 커질수록 

이런 일반 큐와 우선순위 큐 사이의 중복갱신 횟수가 일반 큐가 월등히 많아지게 된다. 
그러므로 최종적으로 일반 큐에서는 O(E+V^2)에서 우선순위 큐 사용 시 O(ElogV)으로 시간상의 이점이 발생하게 된다. 
(V는 정점 수, E는 엣지 수)

Reference

Recommend

Index