Gidhub BE Developer

B-트리

2018-06-13
goodGid
파일처리

B-트리

  • 균형된 m-원 탐색 트리
    • 가장 많이 사용되는 인덱스 방법
  • 차수가 m인 B-트리의 특성은? (m원과 거의 비슷하다.)
    1. 공백이거나 높이가 1 이상인 m-원 탐색 트리
    2. 루트와 리프를 제외한 내부 노드
      • 최소 upper_bound(m/2), 최대 m개의 서브트리
      • 적어도 upper_bound(m/2)-1개의 키 값
    3. 루트 : 리프가 아니면 적어도 두 개의 서브트리를 가짐
    4. 모든 리프는 같은 레벨

m차 B-트리 노드 구조

B-트리 장점

  • 삽입, 삭제 뒤에도 완전 높이 균형 상태 유지

  • 저장 장치의 효율성 : 각 노드의 반 이상 키 값 저장

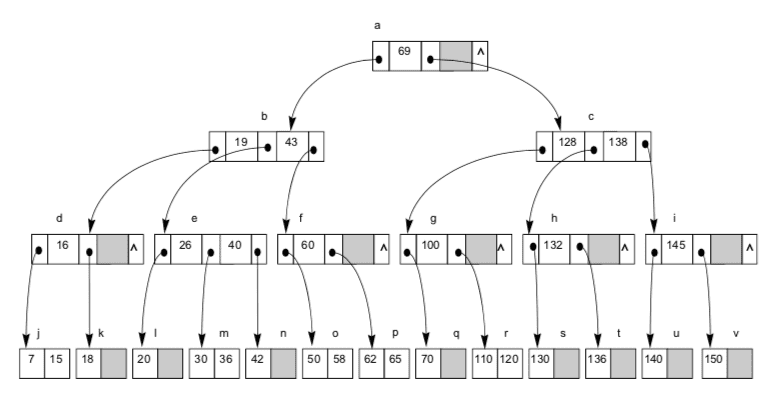
3차 B-트리 구조

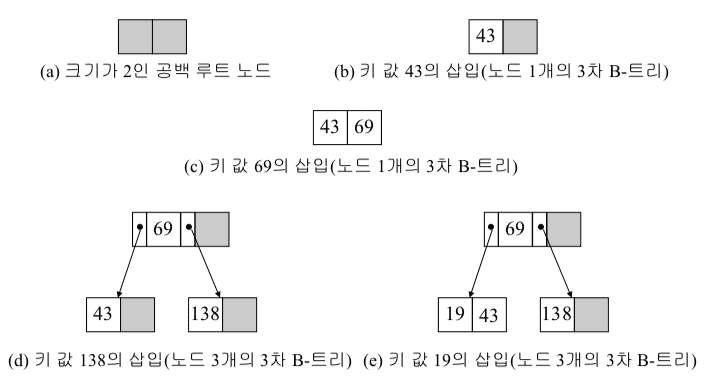
3차 B-트리 삽입

  • 43, 69, 138, 19 순서로 삽입

B-트리 삭제

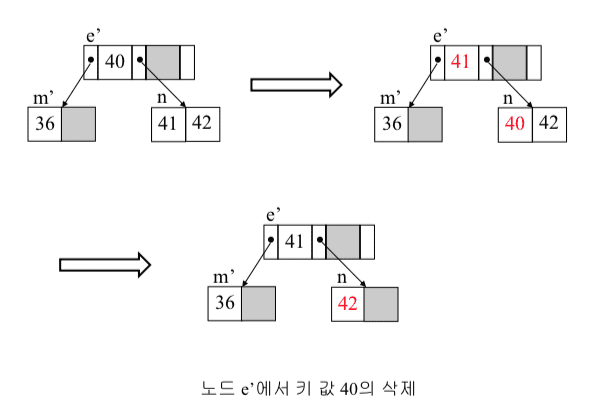
  • 삭제될 키 값이 내부노드(리프가 아닌 노드)에 있는 경우

    • 이 키 값의 후행 키 값(삭제하려는 값 보다 큰 값)과 교환 후
      리프 노드에서 삭제

    • 후행 키 값 대신 선행 키 값 사용 가능

    • 리프 노드에서의 삭제 연산이 더 간단


  • 최소 키 값 수(upper_bound(m/2) - 1) 보다 작은 경우 : underflow

  • 재분배 (Redistribution)

    • 최소 키 값보다 많은 키를 가진 형제 노드에서 차출

    • 부모 노드에 있던 키 값을 해당 노드로 이동,
      빈 자리에 차출된 형제 노드의 키값을 이동

    • 트리 구조를 변경 X

  • 합병 (Merge)

    • 재분배가 불가능한 경우에 적용

    • 형제 노드와 합치는 방법으로, 합병 결과 빈 노드는 제거

    • 트리 구조 변경 O

B-트리 삭제 예 (1)

  • 58, 7, 60, 20, 15 삭제

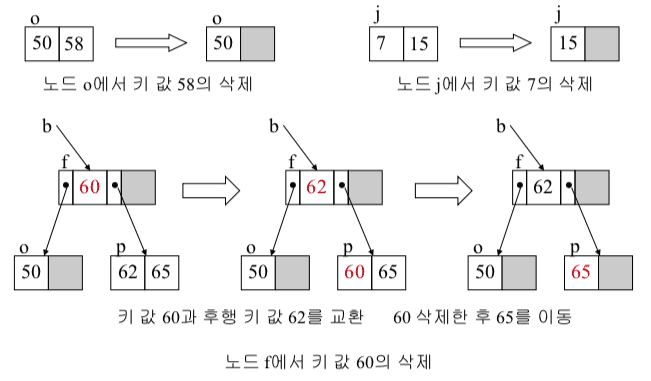
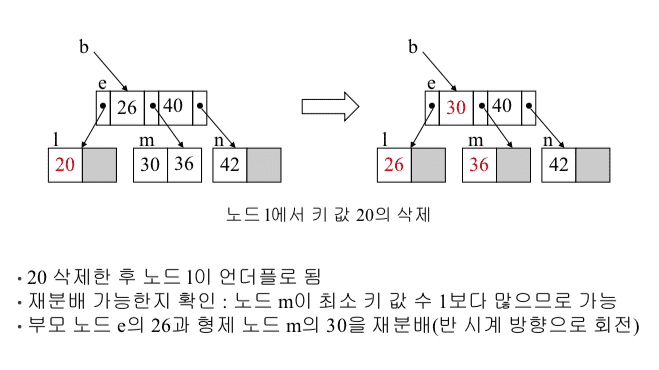
B-트리 삭제 예 (2)

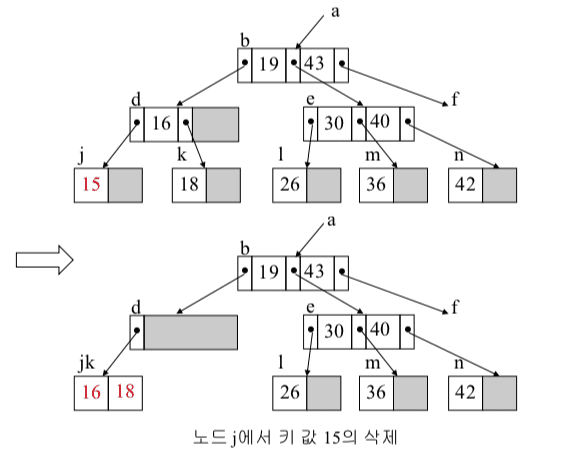
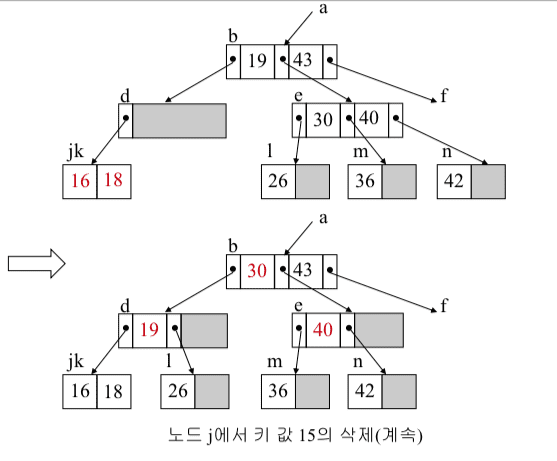
B-트리 삭제 예 (3)

B-트리 관련 참고 자료

Recommend

Index