해시(Hash) 테이블이란?
-
해쉬 테이블은 Key에 Value를 저장하는 데이터 구조이다.
-
function(Key) = Value
-
Key값으로 Value를 찾는데 O(1)시간에 작동한다.
-
해쉬 테이블의 기본 개념은 다음과 같다.
-
Key : 이름
Value : 전화 번호
Size : 16 일 경우 -
John Smith이란 이름을 저장할 때
Key에 해당하는 Index를 찾는 방법은 해시 함수를 호출하면 된다. -
Hash Function(“John Smith”)
–> 해시 함수안에서는 해당 키값을 Size(=16)으로 나눠 Index를 반환한다. -
해시 함수를 통해 Index값을 구한 후
해당 위치에 Value를 저장한다.
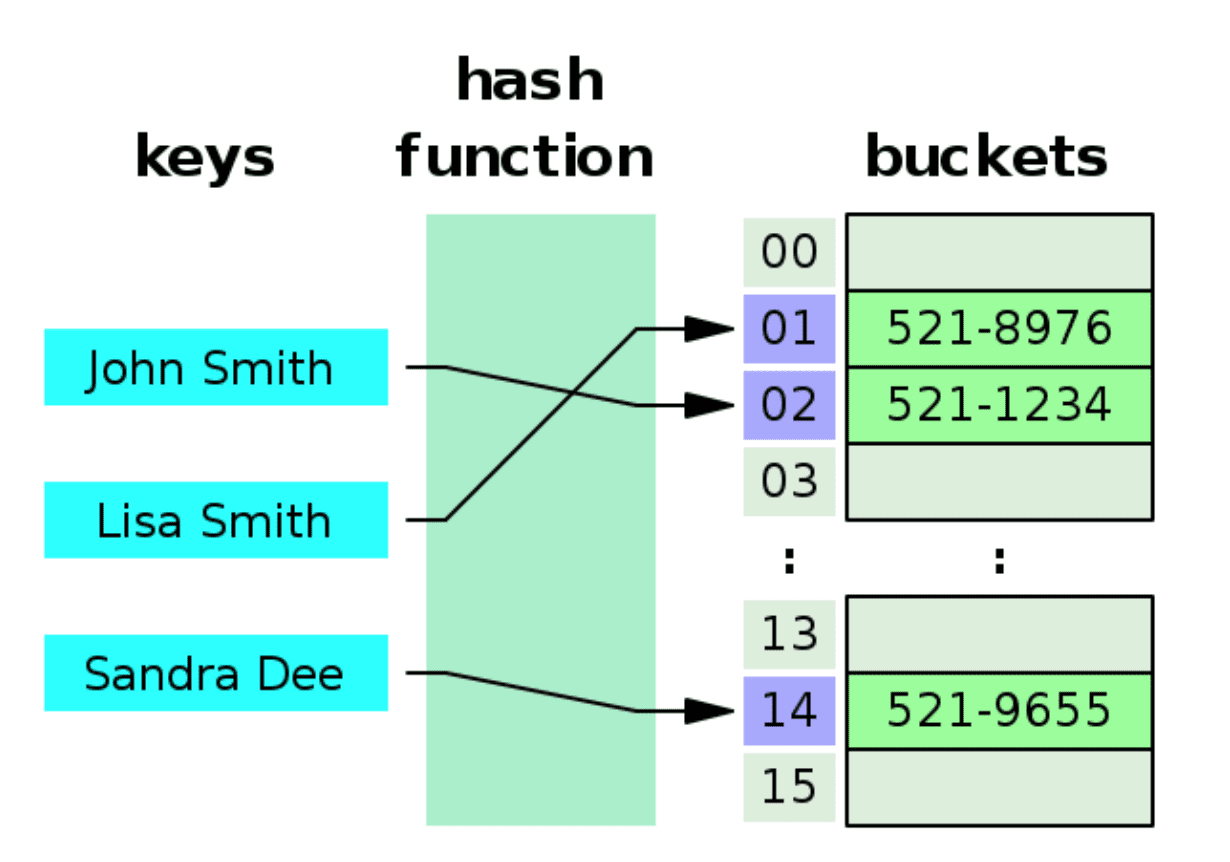
- 이런 형식으로 데이터를 저장하면
Key에 해당하는 Value를 찾기위해 해시 함수를 1번만 수행하면 되기 때문에
데이터의 저장과 삭제가 매우 빠르다.
충돌 처리 알고리즘
-
해쉬 테이블 문제는 근본적인 문제가 존재한다.
-
해시 함수에 의해 정해지는 Index가 중복될 수 있다.
예를 들어
키값이 5, 15, 25이고
해시 버킷의 사이즈가 10이라면
키 5에 해당하는 인덱스는 5
키 15에 해당하는 인덱스는 5
키 25에 해당하는 인덱스는 5와 같은 상황이 발생한다.
-
위와 같은 상황을 충돌(Collision)이라고 한다.
-
충돌을 해결하는 알고리즘에 대해 알아보자.
Separate chaining
-
JDK 내부에서도 사용하고 있는 충돌 처리 방식인데 Linked List를 이용하는 방식이다.
-
각 Index에 데이터를 저장하는 Linked list에 대한 포인터를 가지는 방식이다.
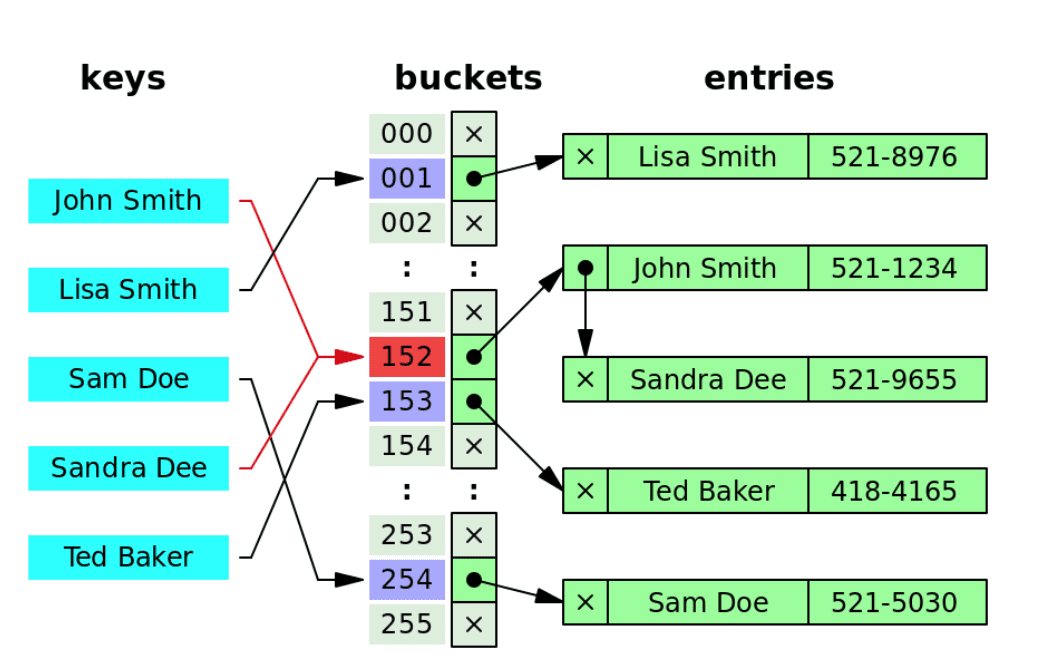
-
만약에 동일 Index로 인해서 충돌이 발생하면
그 Index가 가리키고 있는 Linked list에 노드를 추가한다. -
Separate changing 방식은 Linked List 구조를 사용하기 때문에 추가 시 제약사항이 적다.
-
데이터를 저장하는 구조는 Linked List만 사용하진 않는다.
-
Java 8 Hashmap의 경우에는 Index에 노드가 8개 이하일 경우에는 Linked List를 사용하며
8개 이상으로 늘어날때는 Tree 구조로 데이터 저장 구조를 바꾸도록 되어 있다. -
그 이유는 Tree는 Linked List보다 메모리 사용량이 많고
데이터의 개수가 적을 때
Tree와 Linked List의 Worst Case 수행 시간 차이 비교는 의미가 없기 때문이다. -
또한 실제로는 노드의 수에 따른 구조 변화 시
노드의 수는 8과 6으로 2 이상의 차이를 두었다. -
만약 차이가 1이라면 어떤 한 키-값 쌍이 반복되어 삽입/삭제되는 경우
불필요하게 Tree와 Linked List를 변경하는 일이 반복되어 성능 저하가 발생할 수 있기 때문이다.
static final int TREEIFY_THRESHOLD = 8;
static final int UNTREEIFY_THRESHOLD = 6;
-
실제로 데이터가 많아진다면 Linked List보다 Tree가 더 높은 성능을 보이게 된다.
-
그 이유는 해시 함수의 값이 균등 분포(Uniform Distribution)이라면
Linked List에서는 get() 메소드의 기댓값은 E(N/M) 이다. -
하지만 Tree에서의 get() 메소드의 기댓값은 E(log N/M) 이 된다.
-
그렇기 때문에 데이터의 개수가 일정 이상일 때에는
Linked List 대신 Tree를 사용하는 것이 성능상 이점이 있다.
데이터 검색
-
데이터를 찾고자 할 때는 Key에 대한 Index를 구한 후
-
Index가 가리키고 있는 Linked list를 선형 검색한다.
-
해당 Key에 대한 데이터가 있는지를 검색하여 있으면 리턴하면 된다.
데이터 삭제
-
Key를 삭제하는 것 역시 간단하다.
-
Key에 대한 Index가 가리키고 있는 linked list에서 그 노드를 삭제하면 된다.
Open addressing
-
Open addressing 방식은 Index에 대한 충돌 처리에 대해서
Linked List와 같은 추가적인 메모리 공간을 사용하지 않는다. -
대신 Hash table array의 빈공간을 사용한다.
-
그렇기 때문에 Separate chaining 방식에 비해서 메모리를 덜 사용한다.
-
Open addressing 방식도 여러가지 구현 방식이 있는데
가장 간단한 Linear probing 방식에 대해 알아보자.
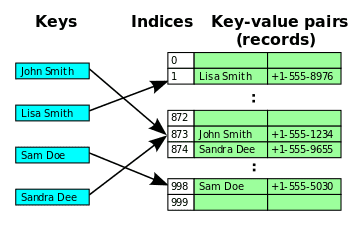
-
위 그림을 보면 “John Smith”와 “Sandra Dee”가 같은 Index를 가리키게 되는 상황이 되면
-
먼저 삽입된 “John Smith”는 정상적인 Index(=873)에 위치하지만
-
나중에 삽입된 “Sandra Dee”는 해시 버킷의 빈 공간의 Index(=874)에 위치한다.
-
만약 874번 Index에 다른 값이 있다면 선형 탐색으로 빈 공간을 찾게된다.
Resizing
-
Open addressing의 경우 고정 크기 배열을 사용하기 때문에 데이터를 더 넣기 위해서는 배열을 확장해야 한다.
-
또한 Separate changing에 경우에도
버킷이 일정 수준으로 차 버리면 각 버킷에 연결되어 있는 List의 길이가 늘어나기 때문에
검색 성능이 떨어지기 때문에 버킷의 개수를 늘려줘야 한다. -
이를 Resizing이라 부른다.
-
Resizing은 별다른 기법이 없다.
-
더 큰 버킷을 가지는 Array를 만든 다음에
새로운 Array에 Hash를 다시 계산해서 복사해줘야 한다.
데이터 검색
-
해시 함수에 의해 나온 Index에 접근을 한다.
-
만약 그 Index의 키값이 찾고자하는 키값이랑 같다면 문제가 안되지만
-
다를 경우엔 다음 Index부터 선형적으로 탐색을 실시한다.
-
탐색의 종료는 해당 key값을 찾거나 모든 key값을 탐색하는 경우이다.
데이터 삭제
-
해시 함수가 해당 키값을 8로 나눈 나머지라고 할 때
10, 18, 26순으로 해시 테이블에 삽입이 된 상태이다. -
Open addressing이기 때문에 3개의 키값(10,18,26)은 Index(=2)를 가리키지만
10은 정상적으로 2번째 Index에 위치
18은 2번째 Index에 이미 값이 있기 때문에 다음 빈 Index(=3)에 위치
26은 18과 동일한 방식으로 그 다음 빈 Index(=4)에 위치한다.

-
이 때 18을 삭제한다.
-
우선 2번 째 Index를 가리키지만 해당 키값이 18이 아니기 때문에
그 다음 버킷을 탐색한다. 다음 버킷의 key값은 18이기 때문에 삭제한다.

-
이제 26을 삭제한다.
-
18과 마찬가지로 2번째 인덱스는 26이 아니기 때문에 다음 버킷으로 이동한다.
-
그런데 여기서 문제가 발생한다.
-
다음 버킷으로 이동 시 바로 전에 18이 삭제되면서 해당 버킷은 빈 공간이 되었다.
-
그렇기 때문에 26을 삭제하는 과정은 여기서 종료가 될 수 있다.
-
이런 상황을 방지하고자 18이 삭제 된 버킷에 임의의 표시를 한다.
-
이 표시가 있을 시에는 그 다음 버킷을 탐색하게 된다.
