- Let’s go deep & wide!
- 9 layers and Tensorboard
- Poor Result
- 해결법 등장 !
- ReLU : Rectified Linear Unit
- ReLU Usage
- sigmoid vs ReLU
- Activation Functions
- Activation Functions on CIFAR-10
Let’s go deep & wide!
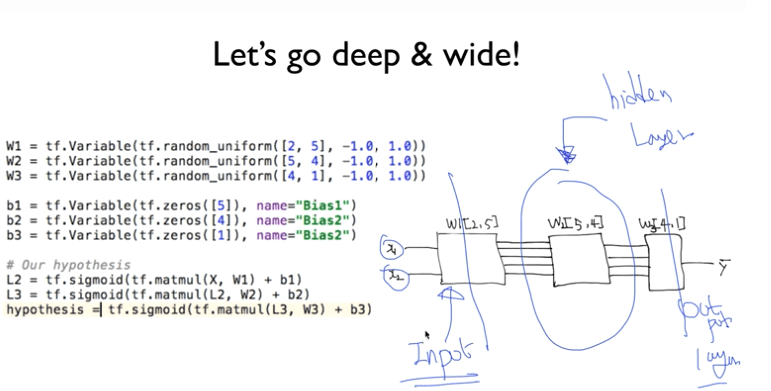
- 3개의 레이어로 구분을 할 수 있다.
- Input Layer
- Hidden Layer
- Output Layer
9 layers and Tensorboard

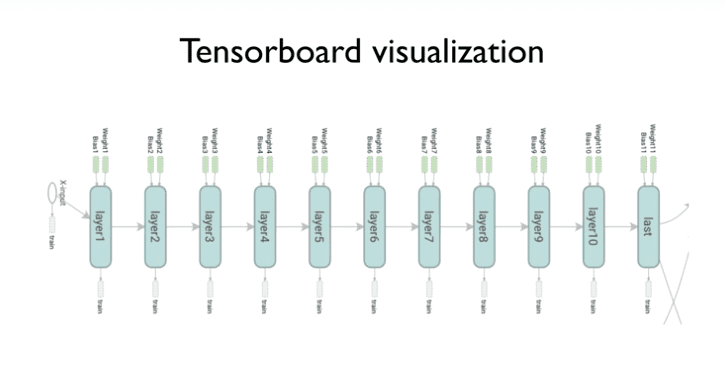
- 각각에 weight값과 어떤 요소가 사용되는지 시각적으로 확인할 수 있다.
Poor Result
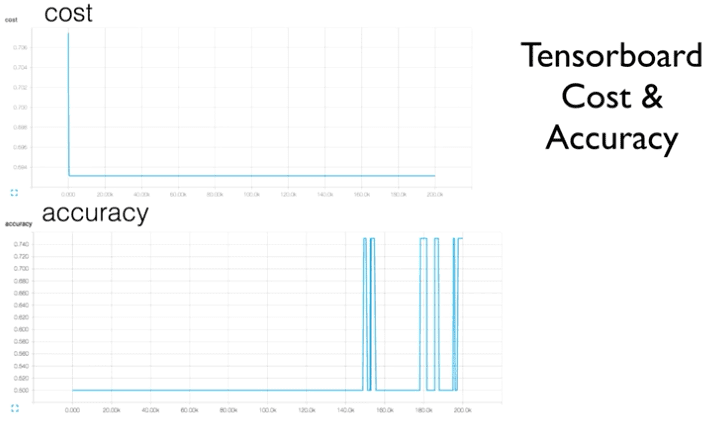
정확도가 0.5라는 절망적인 수치가 나왔다.
(그림이랑은 무관하다. 실제 코드를 돌렸을 때 정확도를 말하는 것이다.)
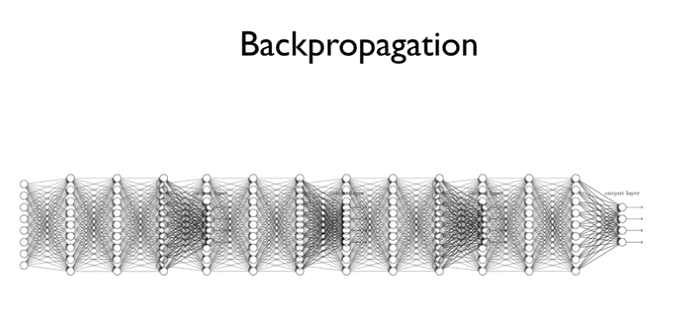
2,3단에 레이어에는 학습이 잘 되지만
그 이상은 학습이 잘 되지 않았다.
뒤에서부터 앞으로
각 layer마다 sigmoid를 통과하기 때문에
sigmoid의 결과값 범위 [ 0 ~ 1 ]라는
아주 작은 값이 지속적으로 곱해지게 된다. ( 0.01 x 0.01 x 0.01 x ~ )
그래서 2~3개의 layer는 괜찮은데
단계를 나아갈때마다
곱해지는 항이 많아지기 때문에
결과값은 계속 작아지고
최종적으로는 Input layer에 가까워질수록
그 값은 0에 가까운 값을 갖게 된다.
즉 Input으로 들어오는 값이
0에 가까운 값을 갖게되는데
그렇게 되면 최종 결과값에 거의 영향을 끼치지 못하게 된다.
이것을 조금 재밌는 말로
Vanishing gradient라 한다.
(괄호안에 winter는 냉각시기, 대중으로 부터 관심이 사라졌다는 뜻이다.)
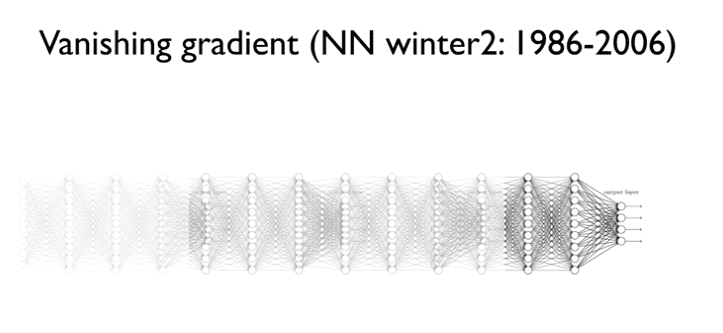
사진을 보면 Input layer갈수록 흐릿해진다.
사진의 선명도는 최종 결과값에 미치는 영향력을 나타낸다.
해결법 등장 !

학자 주장 왈 : sigmoid를 잘못 사용하였다.
sigmoid를 사용하면
항상 1보다 작은 값만 나온다.
그렇기 때문에 지속적으로 곱했을 때
최종적인 값은 굉장히 작아진다.
그러면 어떻게하지 ?
값이 1보다 작아지지 않게 만들자!
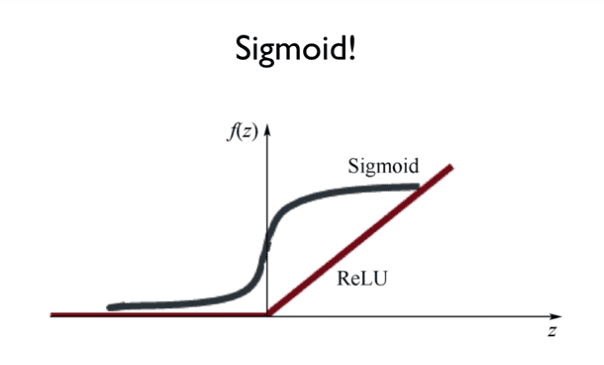
activation을 해야하기 때문에
0보다 작으면 버리고 크면 지속적으로 증가시킨다.
Q. activation을 해야하기 때문에 0보다 작으면 버린다고 하는데 이게 무슨말일까?
기존에 sigmoid를 보면
x < 0일 경우 0에 수렴한다.
그렇기 때문에
ReLU에서 x < 0일 경우 0으로 처리를 해주어도 된다.
ReLU : Rectified Linear Unit
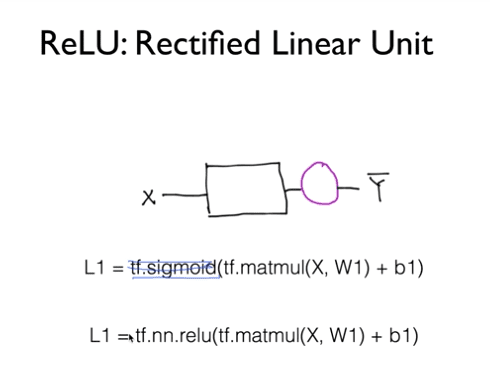
Neural Networks에서는
sigmoid를 사용하는건 좋지 않다.
대신에 tf.nn.relu()를 사용하자.
ReLU Usage

마지막 단에만 sigmoid를 사용한다.
마지막은 [ 0 ~ 1 ] 사이여야하기 때문이다.
그 앞에는 ReLU를 사용한다.
sigmoid vs ReLU

Activation Functions

ReLU를 조금 바꾸면 보다 효율적이지 않을까?
// tanh는 sigmoid를 조금 수정한 버전이다.
Activation Functions on CIFAR-10

- CIFAR-10은 Dataset을 뜻한다.