Gidhub BE Developer

파라메트릭 서치 (Parametric Search)

2017-10-27
goodGid
AlgorithmSkill

To Do

  • 이진 탐색을 활용한 기법이다.

  • 이진 탐색만으로 푸는 문제와 굉장히 비슷한 코드 구조를 띈다.

  • 답이 될 수 있는 해를 이진 탐색으로 계속해서 찾아나가며 Max or Min 값을 구한다.

  • 정답이 될 수 있는 후보가 연속적이여야 한다.

(최솟값을 구하는 경우) 최솟값이 x라면, x이상의 값에 대해서는 모두 조건을 만족
(최댓값을 구하는 경우) 최댓값이 x라면, x이하의 값에 대해서는 모두 조건을 만족

관련 문제

Problem URL : 랜선 자르기

Problem URL : 예산

Problem URL : 나무 자르기

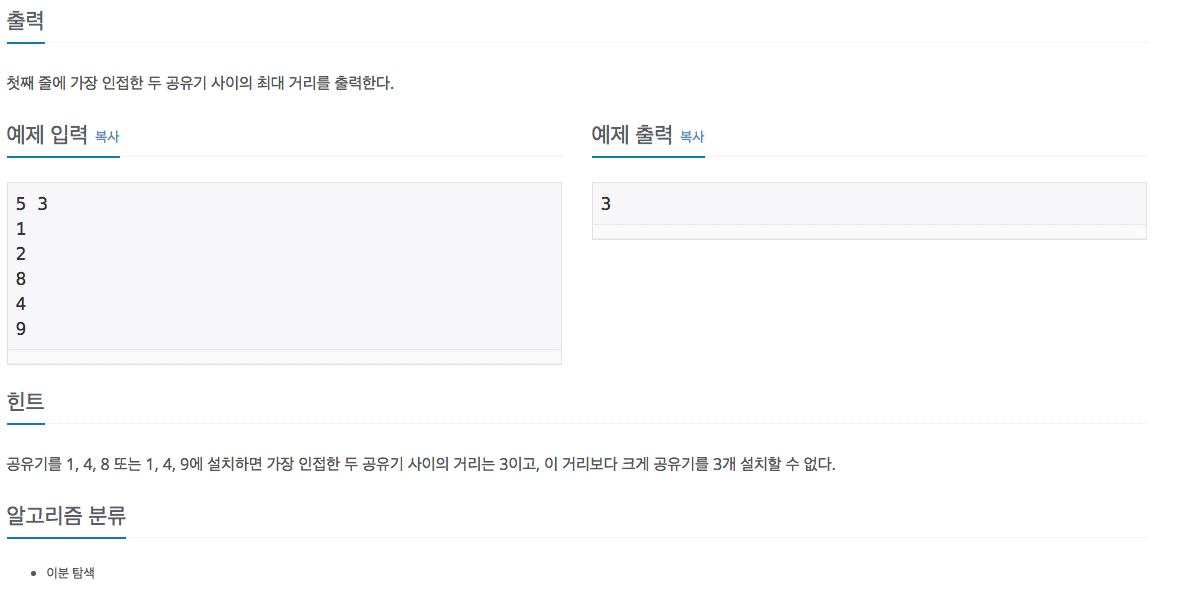
Problem URL : 공유기 설치

Code

  • 공유기 설치 Code
#include <iostream>
#include <algorithm>
#define MAX_SIZE 200000
int pos[MAX_SIZE];

int main()
{
    int n, c;
    scanf("%d %d", &n, &c);
    
    for(int i = 0; i < n; i++)
        scanf("%d", pos + i);
    
    std::sort(pos, pos + n);
    
    int left = 1; // 가능한 최소 거리
    int right = pos[n - 1] - pos[0]; // 가능한 최대 거리
    int ret;
    
    while(left <= right)
    {
        int mid = (left + right) / 2;
        int cnt = 1;
        int start = pos[0];
        
        for(int i = 1; i < n; i++)
        {
            int tmp = pos[i] - start;
            if(tmp >= mid)
            {
                cnt++;
                start = pos[i];
            }
        }
        
        if(cnt >= c) // 실제 설치해야하는 공유기 수 보다 더 많이 설치
                     // -> 간격을 늘려야한다.
        {
            ret = mid;
            left = mid + 1; // 오른쪽 구역에서 최적의 해 찾기
        }
        else right = mid - 1; // 왼쪽 구역에서 최적의 해 찾기
        
    }
    printf("%d\n", ret);
    
    return 0;
}

Feed Back

  • 문제가 힌트다. 최대 거리를 구하라 !
    ==> 거리를 Pivot으로 문제를 풀어라 // 지극히 주관적인 의견임 ㅎㅎ;;

  • 뭔가 100% 내 것으로 만든 느낌이 안든다. 찝찝하게 이해한 느낌 ㅠ____ㅠ (17. 10. 27)

Index