유니온 파인드(Union&Find)란?
-
서로소 집합(Disjoint Set) 또는 병합 찾기 집합(Merge Find Set)이라 불린다.
-
여러 서로소 집합의 정보를 저장하고 있는 자료구조를 의미한다.
예시
- 다음 아래와 같이 원소들이 있다고 가정을 했을 때

- 각각의 원소들이 어떤 원소들과 연결이 되어있는지 입력을 받는다고 가정하면
(1-2, 2-5, 5-6, 5-8, 3-4 이런 방식으로)과 같이 3개의 서로소 집합이 나올 수 있다.

UnionFind Algorithm Process
- Tree 자료구조를 이용하여 위에 있는 서로소 집합( {1,2,5,6,8} {3,4} {7} )을 나타내면 아래처럼 표현이 가능하다.
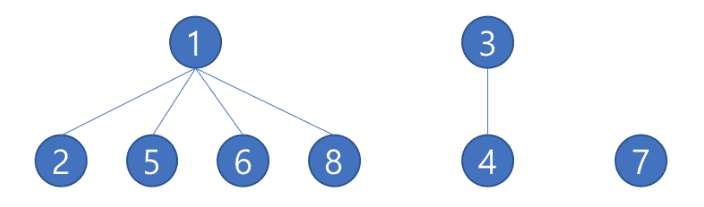
초기화
-
처음에 각각의 원소들은 연결된 정보가 없기 때문에 부모로 자기 자신을 가지고 있다.
즉, parent[i] = i; -
parent[i] : 원소 i의 부모 노드를 가지고 있는 배열, parent[i]는 i의 부모 노드
for(int i=1; i<=n; i++){
parent[i] = i;
}
Find 함수
- Find(x) 함수 : x로 들어온 원소의 Root 노드를 반환한다.
int Find(int x){
// Root인 경우 x를 반환
if(x == parent[x]){
return x;
}
else{
// [1]
// 그 외에는 자신의 루트를 찾으러 간다.
int p = Find(parent[x]);
parent[x] = p;
return p;
// [2] 축약형
// return parent[x] = Find(parent[x])
}
}
-
이때 유니온 파인드를 위해 형성된 트리는 무조건 find함수를 종료할 수 있다.
-
그 이유는 결국 최상위 루트 노드는 자기 자신을 루트 노드로 가리키고 있기 때문이다.
-
이렇게 루트 노드를 찾아 return x를 하게 되면
parent[x]도 return값으로 x를 받으며
모든 노드의 루트 노드를 최상위 노드로 변경시켜 줄 수 있다.
부모 : 1 자식 : 2
부모 : 2 자식 : 3 이라면
parent[2] = 1
parent[3] = 2 이렇게 표현이 가능하다.
이 때
int p = Find(parent[x]);
parent[x] = p;
return p;
이 코드 때문에
parent[2] = 1
parent[3] = 1로 바뀌게 된다.
이해가 안된다면 직접 손으로 해보자 !
- 유니온 파인드를 단순하게 나타낼 수도 있지만, 유니온 파인드 자료구조 또한 Tree 이기때문에
좌측 혹은 우측으로 치우쳐진 트리가 생긴다면 Find()함수 호출 시 매우 오랜 시간이 걸릴 수 있다.
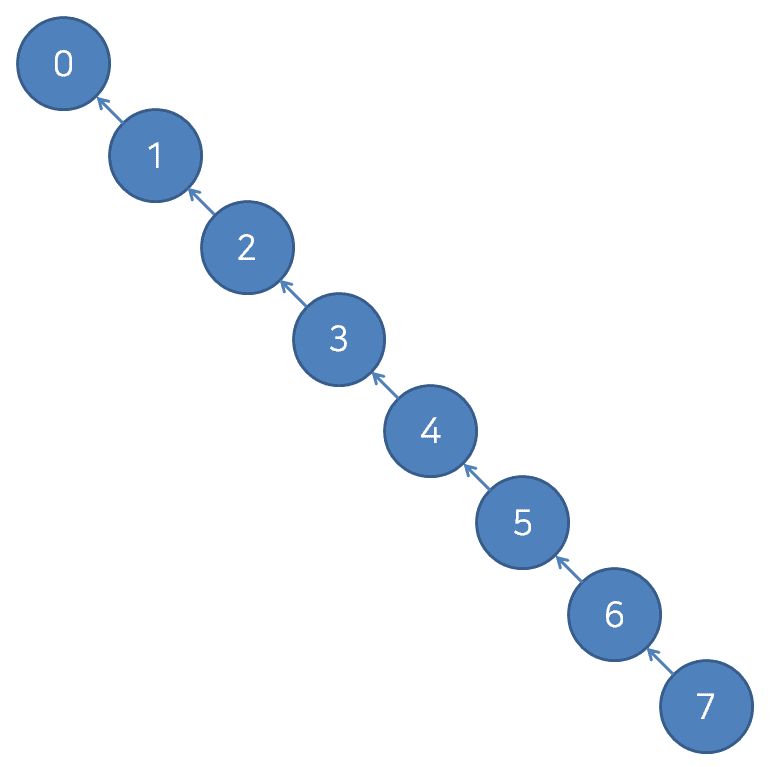
- 이 때 만약 아래 코드와 같이
return parent[x] = Find(parent[x])가 아닌
return Find(parent[x])로 쓴다면 압축되지 않은 유니온 파인드가 된다.
int Find(int x){
// Root인 경우 x를 반환
if(x == parent[x]){
return x;
}
else{
// 그 외에는 자신의 루트를 찾으러 간다.
int p = Find(parent[x]);
return p;
}
}
-
압축되지 않은 유니온에서 Leaf 노드에서 루트를 찾기 위해선 높이만큼 재귀를 해야하는 비효율성이 생긴다.
-
따라서 경로 압축 최적화을 하여 효율성을 추구한다.
여기서 말하는 경로 압축 최적화는 2 코드처럼 했을 경우를 말한다.
Union 함수
-
Union(x,y) 함수 : x원소와 y원소를 합치는 함수로 y의 Root 노드를 x로 한다.
-
Union시 두 개 노드의 level에 따라서 합치는 조건을 추가할 수 있다.
하지만 이 게시글에서는 다루지 않겠다. 궁금하다면 이 블로그를 참고하자!
/*
x와 y의 원소가 들어오면
각각 x에는 들어온 x의 Root 노드 y에는 들어온 y의 Root 노드를 저장해서 비교하고
x에 y를 붙이는 방식 -> y의 Root 노드를 x로 설정한다.
C에서는 Union은 예약어이기 때문에
일반적으로 Merge를 사용한다.
*/
void Merge(int x, int y){
x = Find(x);
y = Find(y);
// 루트가 이미 같다면 같은 트리이다.
if(x == y)
return ;
// 루트가 같지 않다면
if(x != y){
parent[y] = x;
}
}