신장 트리란?
-
신장 트리란 비중있는 그래프 상에서 정점과 정점 사이에 경로를 단일화한 트리를 말한다.
-
그리고 최소 신장 트리(MST, Minimum Spanning Tree)란 정점과 정점 사이의 경로의 합이 최소인 신장 트리를 말한다.
-
그래프에서 MST를 만드는 여러가지 방법 중 많이 알려진 방법으로는 프림 알고리즘과 크루스칼 알고리즘이 있다.
-
프림 알고리즘은 정점을 추가하면서 트리를 확장하는 방법이고,
크루스칼 알고리즘은 간선을 추가하면서 최소 신장 트리를 만드는 방법이다.- 프림은 시작점을 정하고, 시작점에서 가까운 정점을 선택하면서 MST를 구성하므로 그 과정에서 사이클을 이루어지지 않는다.
- 크루스칼은 시작점을 정하지 않고, 최소 비용의 간선을 차례로 대입하면서 MST를 구성하므로,
그 과정에서 사이클이 이뤄지는지 체크해야한다.
사이클을 확인하는 방법으로는 Union-Find(Disjoint-Set) 방법이 있다.
-
그래프에서는 트리와 비슷하게 노드(Node)와 엣지(Edge)로 구성되어 있다.
-
그래프에서는 노드(Node)를 버텍스(Vertex), 엣지(Edge)를 아크(Arc)라고 부른다.
Kruskal Algorithm
-
MST(Minimum Spanning Tree, 최소 신장 트리)이다.
-
그리디(Greedy) 알고리즘이다.
-
가중치가 있는 연결된 무향 그래프의 모든 꼭짓점을 포함하면서 각 변의 비용의 합이 최소가 되는 부분 그래프인 트리이다.
-
한 Vertex를 기준으로 가능한 작은 가중치의 Arc를 사용해서 모든 Vertex를 연결하는 트리를 만든다.
즉, 최소의 Arc 값만 사용해서 모든 Vertex를 연결한다. -
유니온 파인드 (Union-find) 자료 구조를 사용한다.
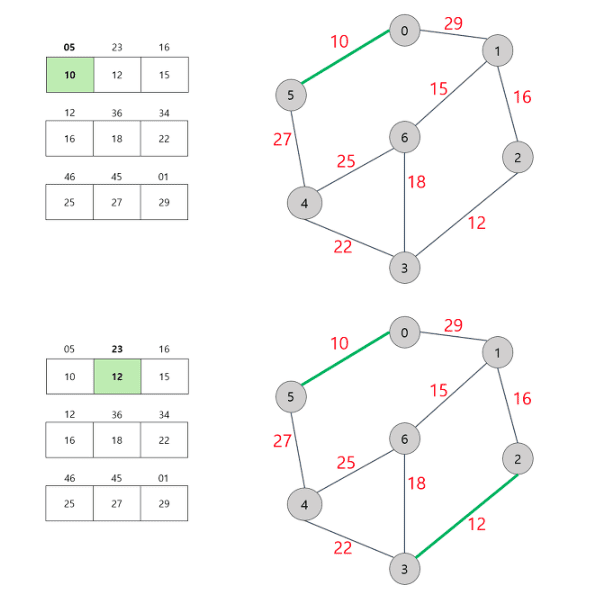
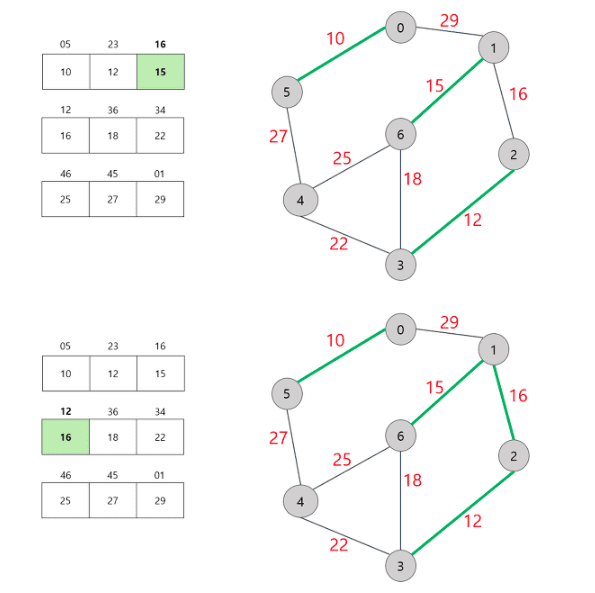
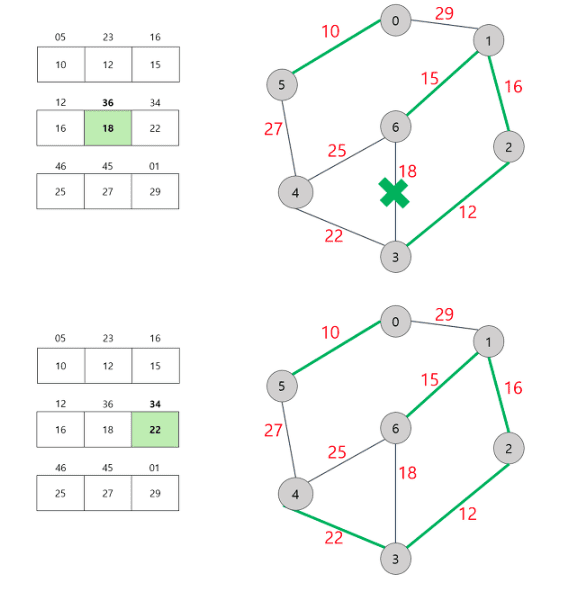
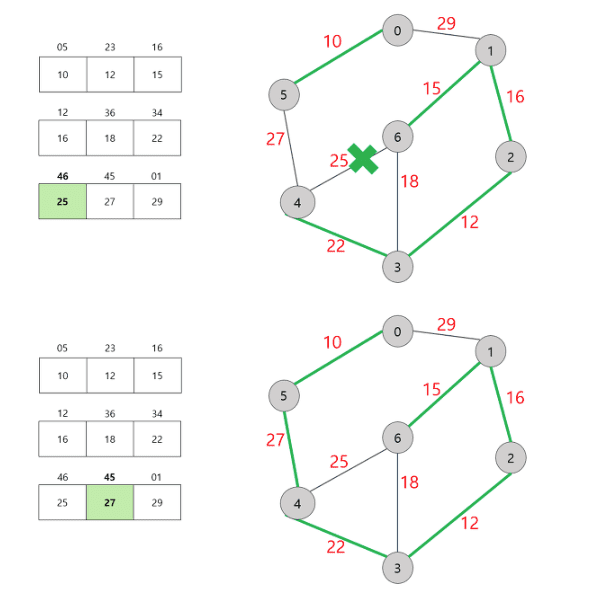
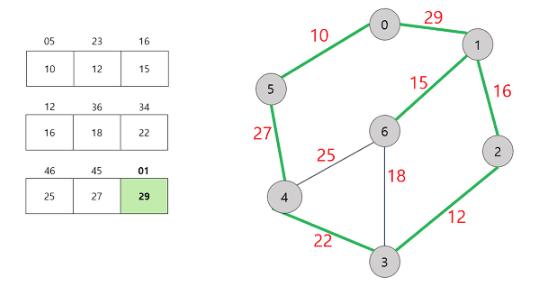
Kruskal Algorithm Process
0. 모든 간선을 끊어 놓는다.
1. 가중치 순으로 간선들을 정렬한다. (오름차순)
2. 정렬된 간선을 순서대로 선택한다.
3. 선택한 간선의 두 정점이 연결되어 있지 않으면, 해당 간선을 최소 스패닝 트리에 포함 시키고 두 정점을 연결한다.
( 1-2-3 처럼 간접적인 연결이어도 1,3 은 연결되어 있는 걸로 친다.)
Q. 최소 신장트리는 최단 경로인가?
-
답은 아니다.
-
예를 들어보자.
-
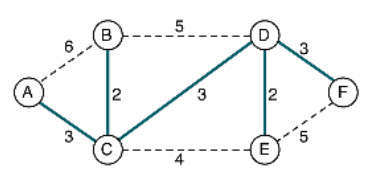
최단 경로처럼 보이지만
A->E가는 길은 최소 신장 트리인ACDE보다ACE가 더 짧다. -
최단 경로를 구하는 알고리즘은 다익스트라 알고리즘을 사용한다.