신장 트리란?
-
신장 트리란 비중있는 그래프 상에서 정점과 정점 사이에 경로를 단일화한 트리를 말한다.
-
그리고 최소 신장 트리(MST, Minimum Spanning Tree)란 정점과 정점 사이의 경로의 합이 최소인 신장 트리를 말한다.
-
그래프에서 MST를 만드는 여러가지 방법 중 많이 알려진 방법으로는 프림 알고리즘과 크루스칼 알고리즘이 있다.
-
프림 알고리즘은 정점을 추가하면서 트리를 확장하는 방법이고,
크루스칼 알고리즘은 간선을 추가하면서 최소 신장 트리를 만드는 방법이다.- 프림은 시작점을 정하고, 시작점에서 가까운 정점을 선택하면서 MST를 구성하므로 그 과정에서 사이클을 이루지 않는다.
- 크루스칼은 시작점을 정하지 않고, 최소 비용의 간선을 차례로 대입하면서 MST를 구성하므로,
그 과정에서 사이클이 이뤄지는지 체크해야한다.
사이클을 확인하는 방법으로는 Union-Find(Disjoint-Set) 방법이 있다.
-
그래프에서는 트리와 비슷하게 노드(Node)와 엣지(Edge)로 구성되어 있다.
-
그래프에서는 노드(Node)를 버텍스(Vertex), 엣지(Edge)를 아크(Arc)라고 부른다.
Prim Algorithm
-
MST(Minimum Spanning Tree, 최소 신장 트리)이다.
-
그리디(Greedy) 알고리즘이다.
-
가중치가 있는 연결된 무향 그래프의 모든 꼭짓점을 포함하면서 각 변의 비용의 합이 최소가 되는 부분 그래프인 트리이다.
-
한 Vertex를 기준으로 가능한 작은 가중치의 Arc를 사용해서 모든 Vertex를 연결하는 트리를 만든다.
즉, 최소의 Arc 값만 사용해서 모든 Vertex를 연결한다.
Prim Algorithm Process
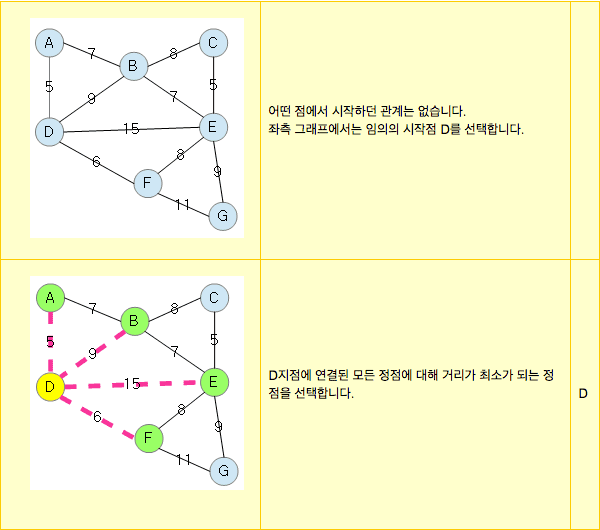
0. 어떤 점에서 시작하던 상관없다.
1. 그래프에서 임의의 하나의 정점을 선택한다.
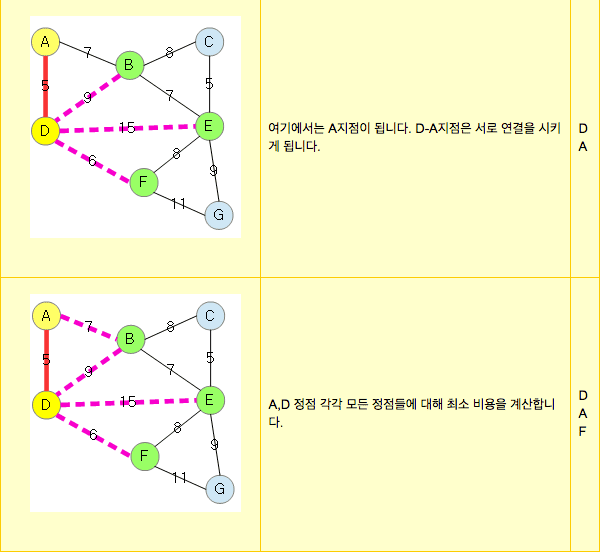
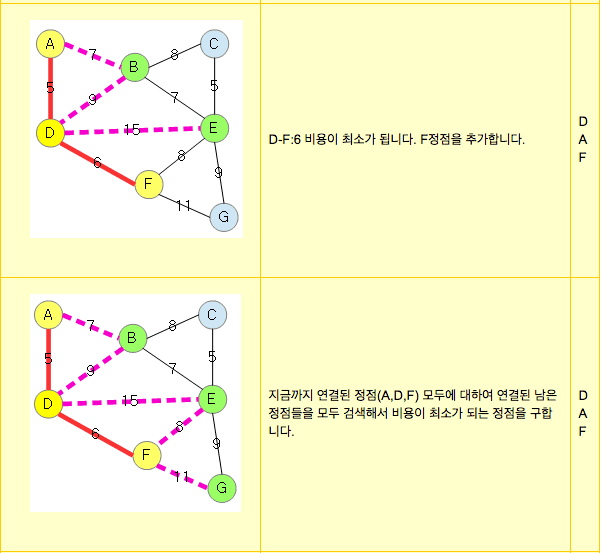
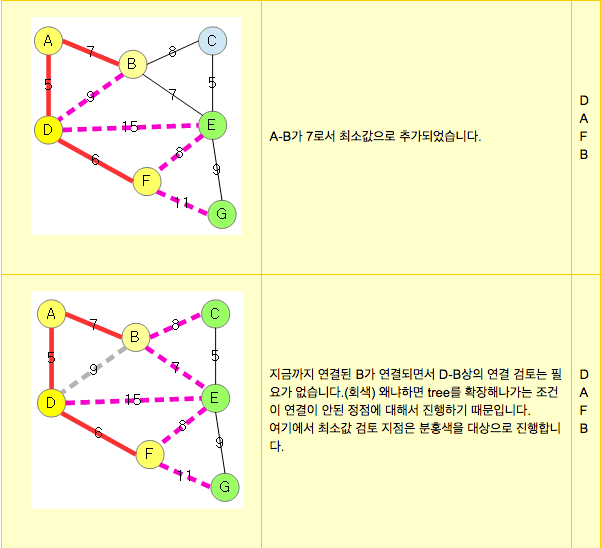
2. 선택한 정점과 인접하는 정점들중 최소 비용의 간선이 존재하게되는 정점을 선택한다.
3. 1,2 과정을 반복 하여 모든 정점이 선택될까지 한다.
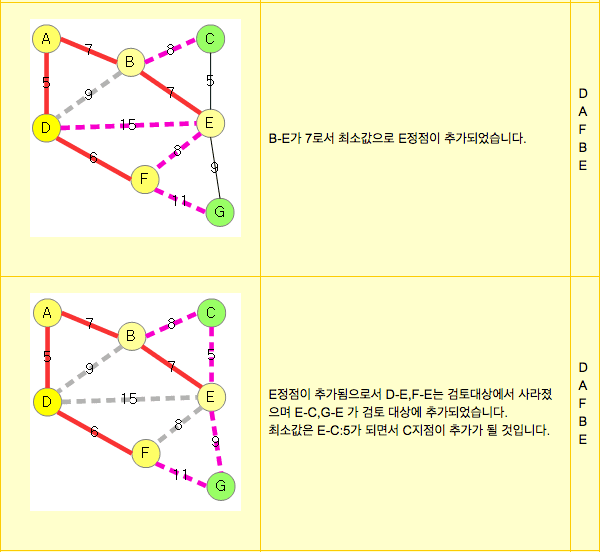
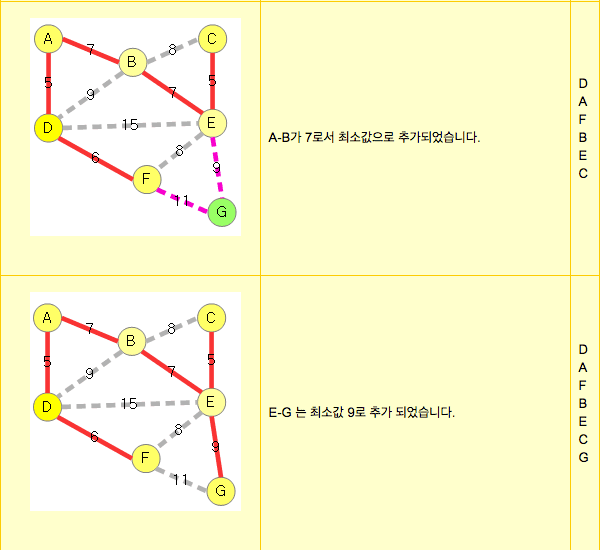
[1] Example